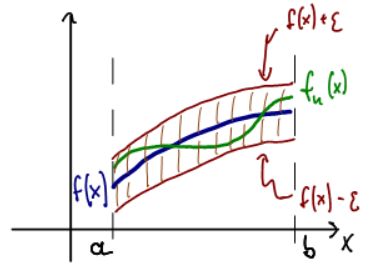
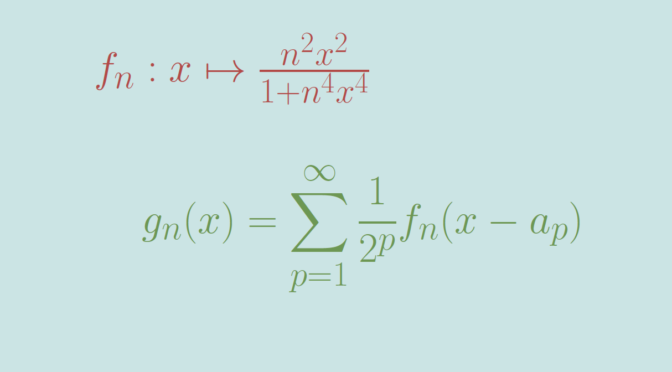real analysis - Question about proof: Uniform cauchy $\Rightarrow$ Uniform convergence - Mathematics Stack Exchange
PDF) On the Uniform Convergence Theorem of Semigroups
Uniform limit theorem - Wikipedia
Uniform convergence in probability - Wikipedia
CS485 Lecture Notes - Summer 2017, Lecture 5 - Independent And Identically Distributed Random Variables, Uniform Convergence, Vaccinia
Show ##\{nx^{n}(1-x)\}_{n = 0}^{\infty}## converges uni | Physics Forums
UCT Definition: Uniform Convergence Theorem | Abbreviation Finder
MathCS.org - Real Analysis: 8.2. Uniform Convergence
Solved 7.17 Theorem Suppose is a sequence of functions, | Chegg.com
Sam Walters ☕️ 在Twitter 上："The #Lebesgue Dominated Convergence Theorem (circa 1908). What I like about it is we don't need the stronger uniform convergence at each point, but merely pointwise convergence
PDF) The Lebesgue Monotone Convergence Theorem
![SOLVED:Tne Fcurier series of f:[ _ T,T] R f(x) = Ixl converges uniformly to since tne Pointwise Convergence theorem applies and f(-T) = f(t). f:[-T,] - R is continuous f(-TT) = f(T)](https://cdn.numerade.com/ask_images/1827d7ffa86f4cb6ab93ae1ba1bbb233.jpg "SOLVED:Tne Fcurier series of f:[ _ T,T] R f(x) = Ixl converges uniformly to since tne Pointwise Convergence theorem applies and f(-T) = f(t). f:[-T,] - R is continuous f(-TT) = f(T)")
SOLVED:Tne Fcurier series of f:[ _ T,T] R f(x) = Ixl converges uniformly to since tne Pointwise Convergence theorem applies and f(-T) = f(t). f:[-T,] - R is continuous f(-TT) = f(T)
nc Problem 2 (4 points each) Practice with pointwise | Chegg.com
Math 3210-3 HW 27 Applications of Uniform Convergence
Dominated Convergence Theorem
Sam Walters ☕️ a Twitter: "It is known that a sequence of functions that converges pointwise on a space X need not converge uniformly on X. But Egoroff's Theorem says that you
On Uniform Convergence in the Wiener‐Wintner Theorem - Arthur Robinson - 1994 - Journal of the London Mathematical Society - Wiley Online Library
real analysis - Counterexample of pointwise convergence - Mathematics Stack Exchange
Theorem relating with uniform convergence - Mathematics Stack Exchange
متكامل للتبرع صنعت لتتذكر uniform convergence of sequence - premiersoccerinstitute.com
10. Read through the following "e-free" proof of the uniform convergence of power series. Does it... - HomeworkLib
real-analysis | Math Counterexamples
Uniform integrability and Vitali's convergence theorem (Chapter 16) - Measures, Integrals and Martingales
